| 地理 第0回 はじめに 応用編
地理の部屋に戻る TOP
統計の読み取り
1.統計の読み取り方
人口・面積・農作物の生産量・貿易など地理の問題では様々な統計の数値・グラフが用いられます。このような統計グラフは読み取るポイントを理解せず,むやみやたらと順位ばかり一生懸命おぼえても意味がありません。もちろん順位そのものに意味がある場合もありますが,順位以上に理解しておくべきことを,これからの講義の中でつかんで下さい。
2.単位と割合
みなさんが統計資料を読み取ろうとするとき,わかっているようでわかっていないのが「単位」と「割合」。これはいわば算数の領域ですが,これがしっかりしていないと問題が解けない場合がある。逆にこれがしっかりしておれば社会の知識がなくても解ける問題がいくらでもあるのです。
①注意力をつける
統計における「単位」とは「長さ」・「重さ」・「量」・「額」を表す記号の単位だけでなく,桁(ケタ)を表す単位があります。統計を読み取るときは,これらの単位は重要な意味をもつという意識を日頃からもちましょう。
②割合なのか量なのか
「割合」とは〔一部〕÷〔全体〕×100ではじきだされ,たいていは「%」で表されます。「一部」を求めるためには〔全体〕×〔割合〕÷100で導き出されます。問題文〔選択肢文〕が「割合」のことをいっているのか,「量」や「額」などをいっているのかによって正確に統計を読み取る必要があります。
以下,実戦形式の問題を紹介しながら説明していきますが,このような問題,「面倒くさい」なんていっているあなたは社会科どころかどの教科の成績も伸びません。ここで必要なのは問題を読み取る「国語」の力,正確に計算する「算数」の力です。国語と算数は勉強の基礎。これはどの教科にも共通することですし,実社会に出ても必要となる力です。これから出てくるさまざまな知識を身につける前にぜひやっておかなくてはならないことで,その意味で私は「第0回」と題して,みなさんに覚悟してもらいたい。
逆にね。知識がなくても解ける問題なら,よろこんで得点するぐらいの気持ちでがんばりましょう。
【例題1】次の資料は日本と韓国の面積・人口・国内総生産の推移を示したものである。資料をみて,あとの問いに答えなさい。[表:応用編0-1 日本国勢図会より]
| |
面積
〔万k㎡〕
2020年 |
人口
〔百万人〕
2020年 |
国内総生産の推移
〔十億ドル〕 |
| 2010年 |
2020年 |
| 日本 |
38 |
126 |
5504 |
5057 |
| 韓国 |
10 |
51 |
1015 |
1637 |
(1)資料から韓国の人口密度は約何人/k㎡ですか。次のア~エから選び,記号で答えなさい。
ア.0.2人/k㎡ イ.5,1人/k㎡ ウ.51人/k㎡ エ.510人/k㎡
(2)資料から読み取れる内容として誤っているものを選び,記号で答えなさい。
ア.日本と韓国を比較すると,人口密度は韓国の方が高い。
イ.日本は韓国に比べて,2020年の一人あたりの国内総生産が多い。
ウ.日本は韓国に比べて,2010年から2020年にかけての国内総生産の増加率が高い。
(1)この問題で問われているのは①人口密度の計算,②桁の単位の読み取りです。
①人口密度は人口÷面積で求めることができます。人口密度の単位「人/k㎡」の「/」は「÷(割る)」を意味していますから,計算式をたてることは難しくありません。
したがって,面積÷人口と式を立て,数値をあてはめただけ(10÷51)で計算したア(約0,2)はまちがっていますね。
②次に正しく人口÷面積の計算式をたてて計算したとします。しかし数値をあてはめただけの51÷10=5.1の計算式と答え(イ)は正しいでしょうか?
表をよくみて下さい。面積の桁単位は「万」です。一方人口は「百万」となっています。これは表に示された数値の一桁目が「万」であり,「百万」であることを示しています。この表の場合,例えば日本の面積の一の位の「8」が「8万」と読み取るのです。つまり「38」は「38万(k㎡)」。日本の人口の一の位は「6」,桁単位は「百万」ですので,「600万」を意味している。そうすると「126」という数値は「1億2800万人」となるのです。
同様に韓国の面積と人口を読み取って,韓国の人口密度を求めてみましょう。韓国の面積は10万k㎡,人口は5100万人。人口密度を求める計算式は51000000÷100000(5100万÷10万)となります。これを計算すると510(人/k㎡)。
(1)答え:エ
このように社会の資料・統計では非常に大きい数値をあつかうため,「0」の数が自然と多くなります。そこで「0」の数を減らすために,上の資料のような方法を使うのです。数値を読み取ったり,計算したりするときはその数値の桁数に注意を払う必要があります。
桁数が大きくなればなるほど,計算が困難になります。計算自体ではなく,「0」の個数や小数点の位置のミス。このミスを極力避けるためには,計算する場所に丁寧に書き取る必要があります。まちがう人の傾向として小さなスペースで,小さな字を書く。練習のときは計算用紙でも用意すればよろしいが,本番のテストではできるだけ広いスペースをみつけて計算することを心がけましょう。一番広いスペースは決まってどこにあるかわかりますか?解答用紙の裏です。
(2)この問題で問われているのは(1)の内容に加えて,③「一人あたりの~」と④「増加率」という考え方です。
選択肢アは(1)の考え方からわかります。日本の人口密度は126000000÷380000=126000000÷380000=12600÷38=約332人/k㎡となり,韓国の方(510)が高いという結果。したがってアは正しい。
③選択肢イは「一人あたりの~」という文になっています。この場合,単純に比べたいもの(この問題の場合は国内総生産)の数値を比較してもダメです。「一人あたり」という場合,人口で割った数値を比較する。2020年の日本の一人あたりの国内総生産は5兆570億ドル÷1億2600万人で計算できます。一方,韓国は1兆6370億ドル÷5100万人となります。ここでも桁の単位を正確に読み取りましょう。
日本の一人あたりの国内総生産=5057000000000÷126000000=約40135ドル
韓国の一人あたりの国内総生産=1637000000000÷51000000=約32098ドル
このように「0」の数の多い計算のコツは共通する「0」の個数を消してしまうことです。
日本の一人あたりの国内総生産=5057000000000÷126000000=約40135ドル
韓国の一人あたりの国内総生産=1637000000000÷51000000=約32098ドル
計算の結果,一人あたりの国内総生産は日本の方が多いのでイも正しい。
④増加率
増加率について理解しておきましょう。「増加率」とは「ある量(変化したあとの量)」が「基準となる量(元の量)」に対してどれだけの割合で増加したかを表す数字です。
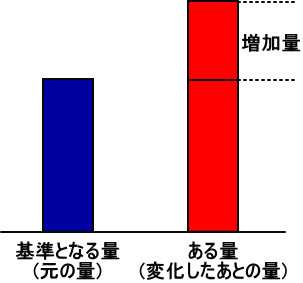
まず「ある量」が「基準となる量」よりどれだけ増えたか,つまり増加量は「ある量-基準となる量」で求まります。この増加量が基準となる量に対してどれだけの割合となるかが増加率です。したがって「増加量÷基準となる量=増加率」となります。これを100分率で表したいときはさらにこの式に「×100」をすればよい。別にしなくてもいいです。
☆増加率=増加量(ある量-基準となる量)÷基準となる量…a
それではこの時点で選択肢ウについて検討してみましょう。この問題の場合基準となるのは2010年の,ある量(変化後の量)は2020年の国内総生産です。
日本の国内総生産の増加率=(5057-5504)÷5504=-447÷5504=-0.08(-8%)
韓国の国内総生産の増加率=(1637-1015)÷622÷1015=0.61(61%)
計算の結果,韓国の増加率の方が高いことがわかりました。したがって,ウが誤り。
(2)答え:ウ
さて,ここで注意するべき点があります。今,日本の国内総生産の増加率を調べたところ,「−(マイナス)」の数値が出てきました。これは別に間違っているわけではありません。増加率が「−」とは,言い換えれば減少したということに他なりません。「増加率が-8%」とは「減少率が8%」という意味だということを理解できるでしょうか。つまりこの問題の場合,日本の増加量が-,韓国の増加量が+であることがわかった時点で次の計算はしなくても結果はわかるのです。
☆増加率の「-」は減少(減少率)を意味する。
さらにここでもう一歩理解を深めてみます。先ほどのaの式を変化してみましょう。このようになります。
☆増加率=増加量÷基準となる量…a
=(ある量-基準となる量)÷基準となる量
=(ある量÷基準となる量)-(基準となる量÷基準となる量)
=(ある量÷基準となる量)-1…b
bの式からわかることは,「-1」は定数です。したがって,実際に計算して比較するのは「ある量÷基準となる量」の部分だけでよいということになります。これは「ある量」が「基準となる量」の何倍かを意味しています。これを「倍率」ともいいます。そうして問題に照らし合わせると,
日本の国内総生産の倍率=5057÷5504=0.91(倍)
韓国の国内総生産の倍率=1637÷1019=1.61(倍)
結果は当然同じとなり,韓国の倍率の方が日本より高くなりました。(日本の場合,倍率が1を下回っている。つまり基準とな年より減少していることがわかる。例えば100の0.9倍は90。)
☆増加率の比較は倍率を比較してもよい。
増加率に関する問題は,統計の読み取りには必須の問題です。その場合特に社会の知識が必要なく解ける問題も含まれています。計算して検討の必要がある場合,増加率と倍率のどちらで検討してもかまいません。いずれにせよ「増加率」という言葉のもつ意味をしっかりと理解をしておきましょう。
☆統計でよく使われる「国内総生産」・「国民(総)所得」
その国の経済力をはかる数値に国内総生産や国民総所得(国民所得)というのがあります。正確に定義できなくてもかまいません。文字通りにとらえておきましょう。「国内総生産」とは,その国の国内で1年間に生産された製品やサービスを合計した額です。国内ですから,国内に住んでいる外国人がつくりだした製品やサービスも含まれます。逆に外国にいる日本人の分は含まれません。額が大きいほど経済力が大きく,小さいほど経済力が小さい。「国民総所得」も少し意味合いは違いますが,両方とも国(国民)の経済力を示す数値だと考えて下さい。
【例題2】次の資料は日本と韓国との間の貿易品の構成を示しています。この資料からわかることを述べた次の文のうち,誤っているものはどれですか。記号で答えなさい。[グラフ:応用編0-2 日本国勢図会2022/23より 2020年]

ア.日本と韓国との間の貿易において,韓国は貿易赤字となっている。
イ.日本が韓国から輸入する鉄鋼の割合は,日本から韓国へ輸出する鉄鋼の割合を上回っている。
ウ.日本の韓国からの機械類の輸入額は,韓国への機械類の輸出額を上回っている。
この問題で注意するポイントは「額」か「割合」かです。
選択肢アは,「韓国」が主語になっています。しかしグラフはともに日本からみた貿易(輸出と輸入)です。輸出額>輸入額なら「黒字」,輸出額<輸入額なら「赤字」ですね。輸出総額と輸入総額は円グラフの上に書かれていて,これをみると日本の輸出総額(4兆7670億円)の方が,輸入総額(2兆8400億円)より多い(総額の桁は10億円)。つまり日本の貿易黒字です。これを逆に韓国からみると,韓国の貿易赤字となります。したがってアは正しい。
選択肢イは,「割合」が主語になっています。この場合グラフをみて,単純に「(鉄鋼の)割合」だけを比べればよい。「韓国から輸入する鉄鋼の割合」=9%,「韓国へ輸出する鉄鋼の割合」=7%なので,イも正しい。
一方,選択肢ウは「額」が主語になっています。そこで割合だけをとって比べることができません。つまり機械類の輸入割合=26%と機械類の輸出割合=40%を比べても意味がない。そうするとグラフ中央の総額を使って計算する必要があります。(額の桁単位は10億円であることに注意して)
韓国からの機械類の輸入額=2兆8400億円×26÷100=7384億円
韓国への機械類の輸出額=4兆7670億円×40÷100=1兆9068億円
計算の結果,韓国への機械類の輸出額の方が多いことがわかりました。したがってウは誤り。
※計算をしなくても,全体額と機械が占める割合の両方が多いことから,機械の輸出額の方が多いことに気づける人は,それでも大丈夫です。
答え:ウ
☆統計を読み取るときの心構え
・何を主語として考えているかによって,統計の読み取り方が変わってくる。
・じっくりと問題と資料を読み取り,書かれている数値だけに飛びつかない。
・狭いスペースで計算しない。→できるだけ広いスペースを見つける。計算問題は解答用紙の裏面が最適。
ではもう一問例題を解いてみましょう。
【例題3】次のグラフは中国・アメリカ・オーストラリア・サウジアラビアからの輸入総額および輸入品目別割合を示している。このグラフについて述べた文として適当なものを,ア~エから選び,記号で答えなさい。
[グラフ:応用編0-3 日本国勢図会2022/23より 2020年]
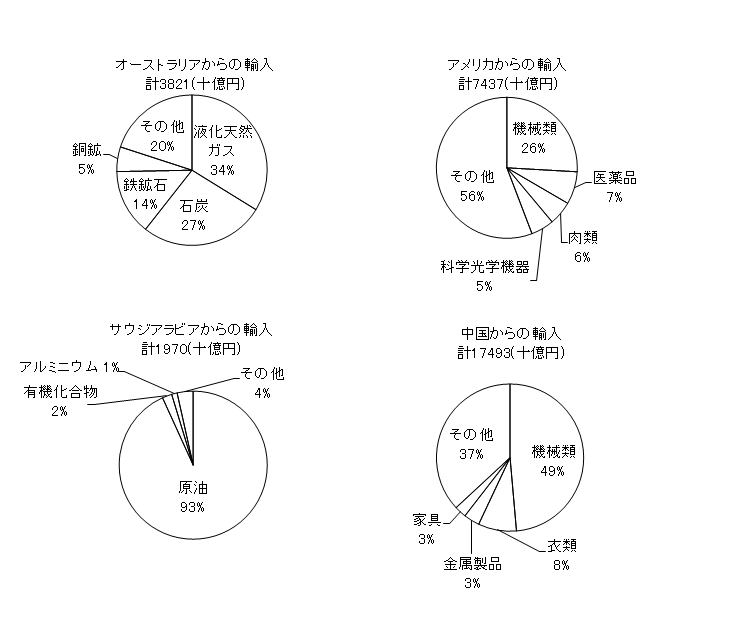
ア.日本の4か国からの輸入品目の割合を比べると,上位2品目の割合の合計がもっとも多い国はサウジアラビアであり,上位2品目の割合がもっとも少ない国は中国である。
イ.日本の4か国からの輸入品目のうち資源では,輸入額がもっとも多いものは液化天然ガスであり,輸入額が2番目に多いものは原油である。
ウ.日本の4か国からの輸入品目の割合を比べると,上位2品目の割合の合計が50%をこえる国が3か国あり,そのうち上位2品目の輸入額の合計がもっとも多い国は中国である。
エ.日本の4か国からの輸入品目のうち工業製品では,輸入額の合計がもっとも多いものは機械類であり,輸入額の合計が2番目に多いものは医薬品である。
・選択肢ア…誤
「割合」のみを考えればよい文です。それぞれのグラフの上位2品目の割合を合計して比べればよい。オーストラリアは34+27=61%,アメリカは26+7=33%,サウジアラビアは93+2=95%,中国は49+8=57%。したがってもっとも多い国はサウジアラビアですが,もっとも少ない国はアメリカ。アは誤り。パッと見ただけでもわかりますが,ここでは正確に計算しました。
・選択肢イ…誤
「資源」に限って「額」を比べる文になっています。グラフ中の資源はオーストラリアの「液化天然ガス」・「石炭」・「鉄鉱石」・「銅鉱」,サウジアラビアの「原油」です。液化天然ガスの輸入額は38210億円×34÷100=約12991.4億円(1兆2991億円)。原油の輸入額は19700億円×93÷100=約18321億円(1兆8321億円)となります。オーストラリアからの液化天然ガスより,サウジアラビアからの原油の輸入額の方が多くなりました。したがって輸入額の合計がもっとも多いのは原油,2番目は液化石油ガスなので,イも誤り。
またオーストラリアからの輸入総額はサウジアラビアの約2倍,液化天然ガスの割合は原油の約1/3倍。したがってオーストラリアの液化天然ガスの輸入額はサウジアラビアの原油の輸入額の約2/3倍。と考えることもできます(正確な計算は必要ない)。しかしこういう問題が苦手な人や心配性な人はきっちり計算して問題に慣れるのも大切です。
・選択肢ウ…正
前半が「割合」についての文,後半が「額」についての文となっています。選択肢アより上位2品目の割合の合計が50%以下の国はアメリカだけなので,「3か国あり,」の部分は正しい。では上位2品目の輸入額はどうでしょう。きっちりと計算式をたてると,
オーストラリア…38210億円×61÷100=約23301億円
サウジアラビア…19700億円×95÷100=約18715億円
中国…174930億円×57÷100=約99710億円
となり,中国からの上位2品目の輸入額がもっとも多いことがわかりました。したがってウは正しい。
数字の感覚に鋭い人は,中国との輸入額はオーストラリアの約5倍,サウジアラビアの約10倍なので,中国の上位2品目の輸入額の合計は他国よりも大きくなることは,計算をしなくても予測がつくかもしれません。
・選択肢エ…誤
「工業製品」にかぎって「額」を比べる文です。まず「機械類」もっとも多いことは疑いようがありません(輸入総額の多い中国とアメリカの,ともに輸入品目割合が1位)。計算してもいいのですが,計算するまでもないでしょう。念のため計算式は
中国からの機械類の額+アメリカからの機械類の額
=(174930億円×49÷100)+(74370億円×26÷100)=約85715+約19336億円=約105051億円(10兆5051億円)
次に中国の「衣類」とアメリカの「医薬品」ではどちらが多いでしょう?
中国からの衣類の輸入額=174930億円×8÷100=約13994億円。
アメリカからの医薬品の輸入額=74370億円×7÷100=約5205億円
したがって輸入額の合計が2番目に多いものは「医薬品」ではなく,「衣類」でした。
これも割合がほぼ同じ(8%と7%)なら,輸入総額が大きい方が輸入品目の額が大きくなる。したがって輸入総額が大きい中国の「衣類」の輸入額が大きくなる。と考えてもよい。
答え:ウ
④概数を利用する
さてここまでみてきた中で,社会科の問題ではケタ数の大きい数字を使った計算が必要になることがわかりました。これまでの解説ではほぼまともに計算式と計算結果を表示してきましたが,慣れてきたらもっと計算をすばやく楽にする方法を使いましょう。それは「概数」です。つまりおよその数。
ケタ数の大きい数字では上3ケタ(前から3ケタ目)以降の数字は,誤差の範囲に入ります。したがって上3ケタ目は四捨五入してしまって,上2ケタの数字だけを残して計算すればよい。
もっと数学に自身のある人は,10の累乗を利用してみる。1000=103,10000=104,1億=108,1兆=1012といった方法を使うと0を書く手間も省けます。
【例題3】の統計を使ってやってみましょう。中国からの機械類の輸入額を求めてみます。中国からの総輸入額は174930億円です。上2ケタの概数にすると上3ケタ目(「4」)を四捨五入して,約170000億円です。(さらに10の累乗を使うと170000×108 )。中国からの機械類の輸入割合は49%ですから,2ケタの概数にするとそのまま49%となります。実際の問題では少数第一位まで示されている問題も多く,2ケタの概数にすることで面倒な少数点以下を消すことができます。したがって中国からの機械類の輸入額は,
170000億×49÷100=83300億(約8.33兆円)となります。
10の累乗を利用するには,かなりの数字の感覚が必要となりますが,2ケタの概数は計算を楽にするだけでなく,計算ミスも減らすことができます。是非利用するようにしましょう。
【例題4】次の統計をみて,あとの問いに答えなさい。
1.資料中の国のうち,国民1人あたりの国内総生産が2番目に少ない国はどこか。国名を答えなさい。
2.資料から読み取れることについて述べた文として正しいものを選び,記号で答えなさい。
ア.資料中の国のうち,人口3位の国と発電量3位の国は同じである。
イ.国内総生産と観光収入は相関関係にあり,国内総生産が多いほど観光収入も多くなっている。
ウ.発電量の多い上位2ヶ国は,どちらもAPECに加盟している。
エ.穀物生産量の多い上位2ヶ国は,どちらもBRICSに含まれる新興国である。
1.問題は「1人あたりの国内総生産」とありますから,「国内総生産」だけを比較しても意味がありません。「1人あたりの国内総生産」は国内総生産÷人口で求めることができます。ただし国内総生産の桁は「億ドル」,人口は「万人」です。万の桁に統一して計算します。式は以下の通り。
カナダ…171260000万÷3774万
ブラジル…186860000万÷21256万
フランス…277890000万÷6527万
エジプト…24980000万÷10233万
インド…277940000万÷138000万
オーストラリア…145390000万÷2550万
これいくら万と万が約分できるからといっても,計算するのがいやになりますね。そこで計算をぐっと簡単にするため2桁の概数をつかってみる。上3桁目を四捨五入してみましょう。
カナダ…180000000万÷3800万
ブラジル…190000000万÷21000万
フランス…280000000万÷6500万
エジプト…25000000万÷10000万
インド…280000000万÷140000万
オーストラリア…150000000万÷2600万
かなり余計な数字が消えましたね。さらに余分な0を約分して消してしまいましょう。
カナダ…1800000÷38
ブラジル…190000÷21
フランス…2800000÷65
エジプト…2500÷1
インド…28000÷14
オーストラリア…1500000÷26
これ全部計算してもいいんだけど,ここまで簡単にしてしまうと計算結果が下位2ヶ国は,0の数を比較すればわかります。(もちろんきちんと計算して,結果を比較してもかまわない)エジプトとインドですね。エジプトは2500ドル,インドは2000ドル。1人あたりの国内総生産が2番目に低いのはエジプトでした。
※ここでは計算だけに焦点をあてて解説しましたが,問題は「1人あたり国内総生産」の低さを比べる問題なので,言い換えれば,最初から発展途上国だけを探し出して比較すればよい。発展途上国はアジア・アフリカに多いので資料の中ではインドとエジプトに絞って計算に取り組めばよい。この2ヶ国を2桁の概数を利用すると,計算は実に簡単に住む。(念のためにブラジルを加えても6ヶ国すべてを確認する必要はない)
2.すべて表中の数値の比較で解ける。
ア(誤)…人口3位の国はエジプト,発電量3位はブラジル。
イ(誤)…国内総生産1位のインドは,観光収入では3位である。
ウ(誤)…発電量上位2ヶ国はインド,カナダ。APECはアジア太平洋経済協力会議。インドは加盟していない。
エ(正)…穀物生産量上位2ヶ国はインド・ブラジル。BRICSはブラジル,ロシア,インド,中国,(南アフリカ共和国)なので正しい。
答え:1.エジプト 2.エ
3.凡例にしたがって作図する問題
公立高校の入試問題ではよく見かける問題です。作図例が示されており,それにしたがって与えられた図や模様を書いていく問題。次の例題をやってみましょう。
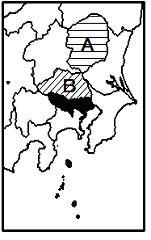
【例題4】次の資料をみて,地図A・Bの県にあてはまる模様を東京の凡例にしたがって地図に書きなさい。
| 都県 |
昼間人口
(千人) |
夜間人口
(千人) |
昼夜間比率 |
| 茨城 |
2799 |
2867 |
97.6 |
| 栃木 |
1914 |
1933 |
99.0 |
| 群馬 |
1939 |
1939 |
100 |
| 埼玉 |
6435 |
7345 |
87.6 |
| 千葉 |
5550 |
6284 |
88.3 |
| 東京 |
16752 |
14048 |
119.2 |
| 神奈川 |
8306 |
9237 |
89.9 |
昼夜人口比率…夜間人口100人に対する昼間人口の割合(昼間人口÷夜間人口×100)
[表:応用編0-4 総務省統計局 令和2年国政調査より]
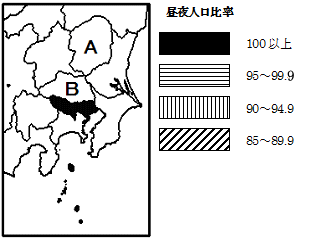
問題の地図には凡例として東京都の模様(黒のぬりつぶし)が書き込まれています。このように地図中A県=栃木県とB県=埼玉県も数値と模様にしたがって書き込むのです。
県の位置さえわかれば「こんな問題まちがいようがない」と思っているでしょう。このような油断がまちがいを招くのです。まずまちがいの解答をみせます。
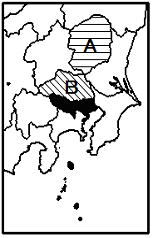
どこがまちがっているかわかりますか?わからない人はこのままだと本番でもまちがいます。B県(埼玉県)の模様は昼夜人口比率が87.6なので斜線ですね。しかし問題の斜線と答えの斜線の方向が違っているのがわかりますか?勝手に解釈してはいけません。斜線ならよいというあまい考えでは話にならない。もちろん作図の問題には様々なパターン(模様・形・線など)があります。知識があるなしに関わらずこのようなまちがいは少しの注意で防げるのです。実際,現場の人間からみていて結構あるのです,この誤答。
答え:
基礎編へ
|





